汉明距离（二十三）

前言

汉明距离广泛应用于多个领域。在编码理论中用于错误检测，在信息论中量化字符串之间的差异。
两个整数之间的汉明距离是对应位置上数字不同的位数。

根据以上定义，我们使用异或运算，记为 ^，当且仅当输入位不同时输出为 1

计算 x 和 y 之间的汉明距离，可以先计算 x ^ y，然后统计结果中等于 1 的位数。

一、题目描述

这是 LeetCode 上的第四百六十一题题：汉明距离，难度为 简单。

Tag：「位运算」

两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。

给你两个整数 x 和 y，计算并返回它们之间的汉明距离。

示例 1：

输入：x = 1, y = 4
输出：2
解释：
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑
上面的箭头指出了对应二进制位不同的位置。

示例 2：

输入：x = 3, y = 1
输出：1

提示：

1、0 <= x, y <= 2^31 - 1

二、解题思路

法一：内置位计数功能

大多数编程语言都内置了计算二进制表达中 111 的数量的函数。在工程中，我们应该直接使用内置函数

代码实现：

class Solution {
    public int hammingDistance(int x, int y) {
        return Integer.bitCount(x ^ y);
    }
}

复杂度分析：

1、时间复杂度：O(1)。不同语言的实现方法不一，我们可以近似认为其时间复杂度为 O(1)。

2、空间复杂度：O(1)。

法二：移位实现位计数

在锻炼算法能力时，重复造轮子是不可避免的，也是应当的。因此读者们也需要尝试使用各种方法自己实现几个具有位计数功能的函数。本方法将使用位运算中移位的操作实现位计数功能。

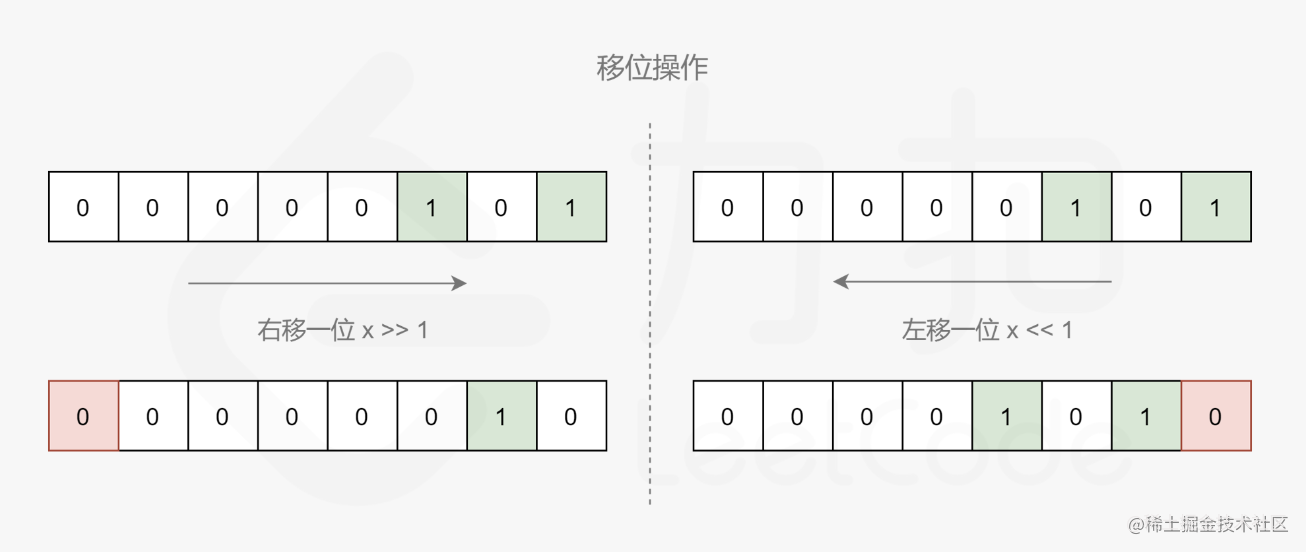
具体地，记 s=x^y，我们可以不断地检查 s 的最低位，如果最低位为 1，那么令计数器加一，然后我们令 s 整体右移一位，这样 s 的最低位将被舍去，原本的次低位就变成了新的最低位。我们重复这个过程直到 s=0 为止。这样计数器中就累计了 s 的二进制表示中 1 的数量。

代码实现：

class Solution {
    public int hammingDistance(int x, int y) {
        int s = x ^ y, ret = 0;
        while (s != 0) {
            ret += s & 1;
            s >>= 1;
        }
        return ret;
    }
}

复杂度分析：

1、时间复杂度：O(logN)，其中 N 是元素的数据范围，在本题中 logN=log2^31=31。

2、空间复杂度：O(1)。

三、总结

本道算法题难度为简单，我们使用了系统内置和移位两种方式进行了实现

好了，本篇文章到这里就结束了，感谢你的阅读🤝