堆

一、堆的定义

堆是计算机科学中一类特殊的数据结构的统称，堆通常可以被看做是一棵完全二叉树的数组对象。

堆的特性:

1）、它是完全二叉树，除了树的最后一层结点不需要是满的，其它的每一层从左到右都是满的，如果最后一层结点不是满的，那么要求左满右不满。

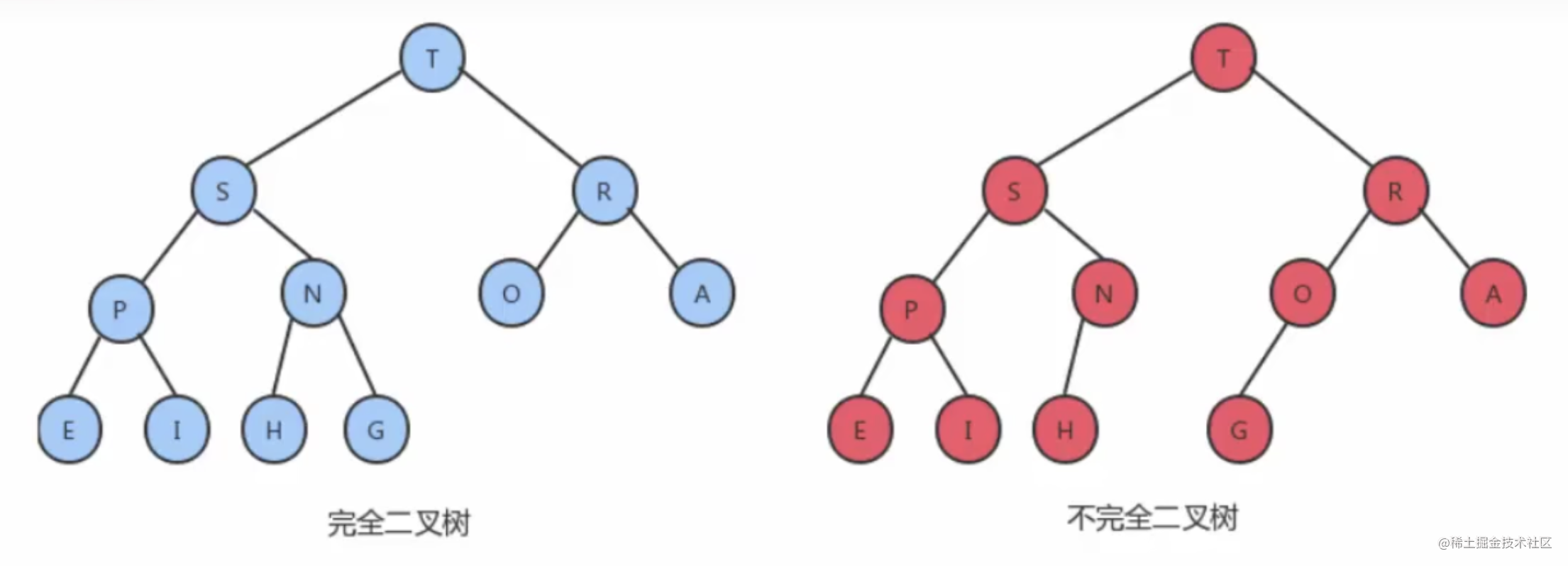
2）、它通常用数组来实现。

具体方法就是将二叉树的结点按照层级顺序放入数组中，根结点在位置 1（之所以不从 0 开始，是为了方便我们索引的操作），它的子结点在位置 2 和 3，而子结点的子结点则分别在位置 4.5.6 和 7，以此类推。

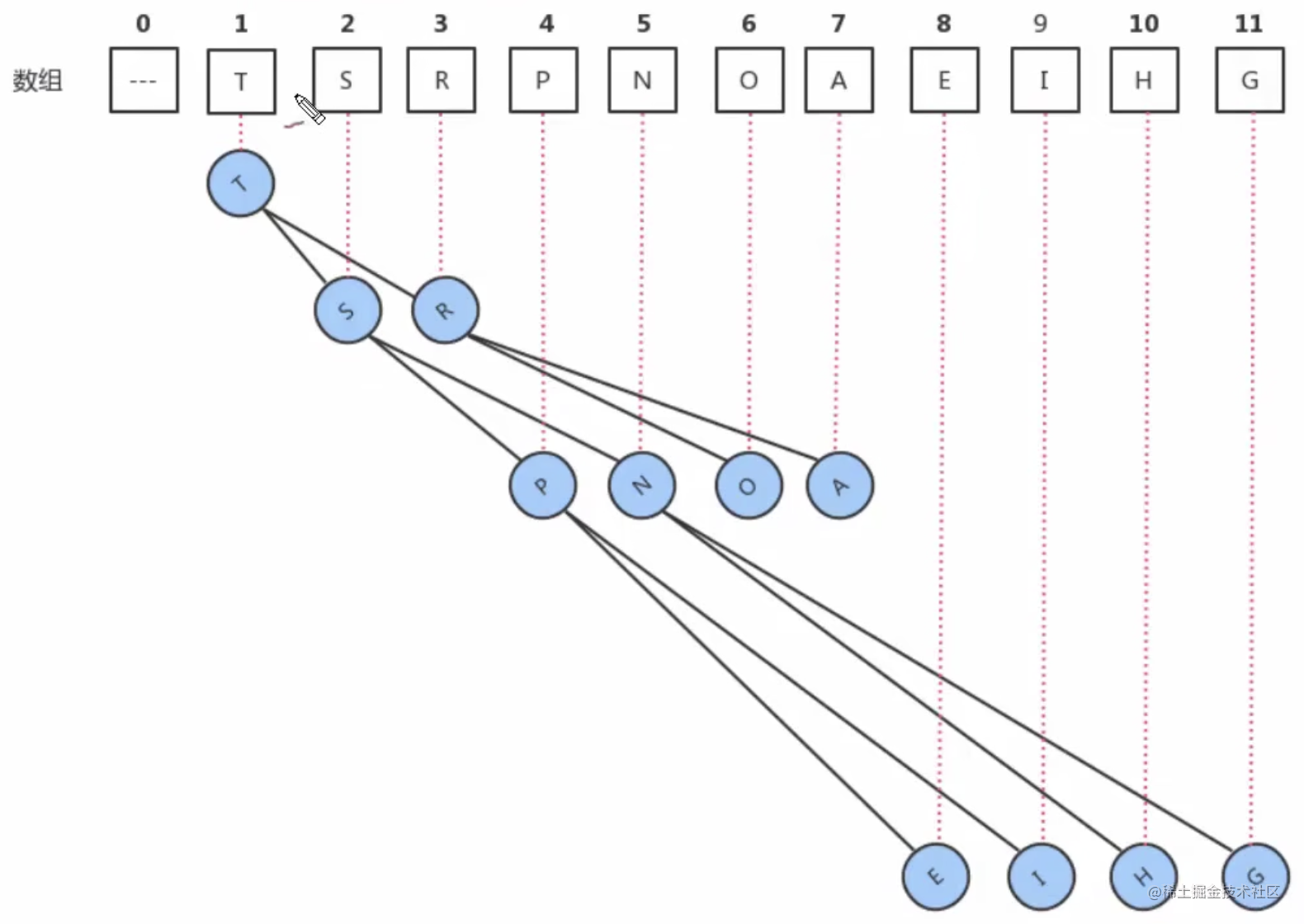
如果一个结点的位置为k，则它的父结点的位置为 k/2 ，而它的两个子结点的位置则分别为 2k 和 2k+1 。这样，在不使用指针的情况下，我们也可以通过计算数组的索引在树中上下移动：从 a[k] 向上一层，就令 k 等于 k/2,向下一层就令 k 等于 2k 或 2k+1。

3）、每个结点都大于等于它的两个子结点。这里要注意堆中仅仅规定了每个结点大于等于它的两个子结点，但这两个子结点的顺序并没有做规定，跟我们之前学习的二叉查找树是有区别的。

二、堆的 API 设计

类名	Heap<T extends Comparable<T>>
构造方法	Heap(int capacity) ：创建容量为 capacity 的 Heap 对象
成员方法	1、private boolean less(int i,int j) ：判断堆中索引处的元素是否小于索引处的元素 2、private void exch(int i,int j) ：交换堆中索引 i 和索引 j 的值 3、public T delMax() ：删除堆中最大的元素，并返回这个最大元素 4、public void insert(T t) ：往堆中插入一个元素 5、private void swim(int k) ：使用上浮算法，使索引 k 处的元素能在堆中处于一个正确的位置 6、private void sink(int k) ：使用下沉算法，使索引 k 处的元素能在堆中处于一个正确的位置
成员变量	1、private T[] items ：用来存储元素的数组 2、private int N ：记录堆中元素的个数

三、堆的实现

3.1、代码实现

public class Heap<T extends Comparable<T>> {

    private T[] items;
    private int N;

    public Heap(int capacity){
        items = (T[]) new Comparable[capacity + 1];
        N = 0;
    }

    private boolean less(int i,int j){
        return items[i].compareTo(items[j]) < 0;
    }

    private void exch(int i,int j){
        T temp = items[i];
        items[i] = items[j];
        items[j] = temp;
    }

    public void insert(T t){
        items[++N] = t;
        swim(N);
    }

    //使用上浮算法，使索引 k 处的元素能在堆中处于一个正确的位置
    private void swim(int k){
        //通过循环，不断比较当前节点和父节点的值，如果父节点比当前节点小则交换位置
        while (k > 1){
            //比较当前节点和父节点
            if(less(k/2,k)){
                exch(k/2,k);
            }
            k = k / 2;
        }
    }

    //删除堆中的最大元素，并返回这个元素
    public T delMax(){
        T max = items[1];
        //交换1和最大索引处的位置
        exch(1,N);
        //将最大索引处的位置置为 null
        items[N] = null;
        //元素个数减1
        N--;
        //让堆重新有序，通过下沉调整堆
        sink(1);
        return max;
    }

    private void sink(int k){
        //循环，不断对比当前 k 和其子节点 2k 及 2k+1 中的较大者的元素大小，如果当前节点小，则交换位置
        while (2*k <= N){
            //获取当前节点的子节点的较大者
            int max;
            if(2*k + 1 < N){
                //证明有右子节点
                if(less(2*k,2*k + 1)){
                    //左子节点小于右子节点
                    max = 2*k + 1;
                }else {
                    //左子节点大于右子节点
                    max = 2*k;
                }
            }else {
                max = 2*k;
            }
            //比较当前节点和较大者的值
            if(!less(k,max)){
                break;
            }

            //交换 k 和 max 的位置
            exch(k,max);

            k = max;
        }
    }
}

3.2、测试

public class HeapTest {

    public static void main(String[] args) {
        Heap<String> heap = new Heap<>(10);
        heap.insert("A");
        heap.insert("B");
        heap.insert("C");
        heap.insert("D");
        heap.insert("E");
        heap.insert("F");
        heap.insert("G");

        String delResult;
        while ((delResult = heap.delMax()) != null){
            System.out.print(delResult + " ");
        }
    }
}

//打印结果
G F E D C B A 

四、总结

本篇文章我们介绍了：

1、堆的特性：

1、它是完全二叉树

2、它主要用数组实现。访问当前 k 节点的父节点为 k/2，左子节点为 2k，右子节点为 2k + 1

3、每个节点大于等于它的两个子节点。注意和二叉树区分开来

2、堆的 API 设计，代码实现，并进行了测试用例测试

好了，本篇文章到这里就结束了，感谢你的阅读🤝