对称二叉树(二十七)
一、题目描述
这是 LeetCode 上的第一百零一题:对称二叉树,难度为 简单。
Tag:「二叉树」、「深度优先搜索」、「广度优先搜索」
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
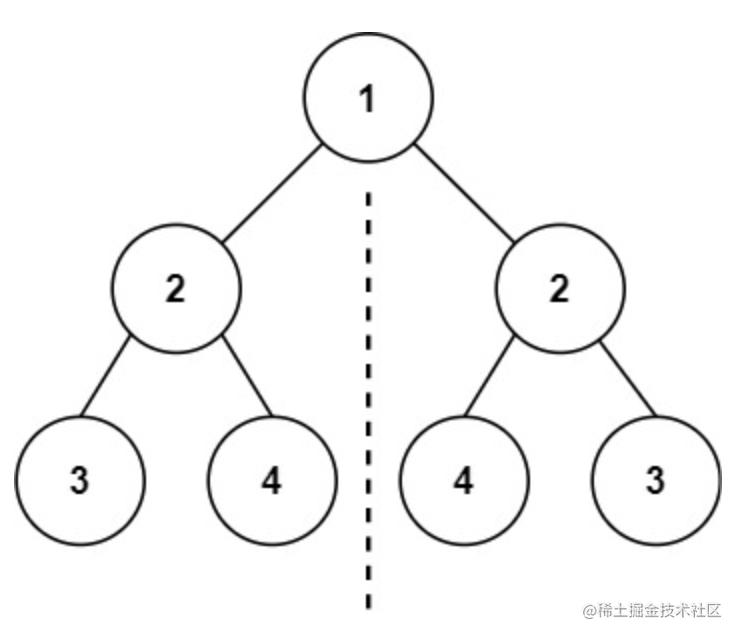
1 | |
示例 2:
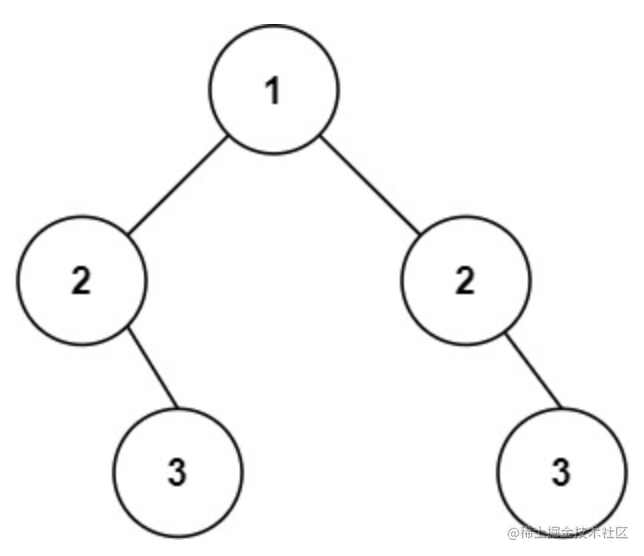
1 | |
提示:
1、树中节点数目在范围 [1, 1000] 内
2、-100 <= Node.val <= 100
二、解题思路
法一:递归
如果一个树的左子树与右子树镜像对称,那么这个树是对称的。
因此,该问题可以转化为:两个树在什么情况下互为镜像?
如果同时满足下面的条件,两个树互为镜像:
1、它们的两个根结点具有相同的值
2、每个树的右子树都与另一个树的左子树镜像对称
我们可以实现这样一个递归函数,通过「同步移动」两个指针的方法来遍历这棵树,p 指针和 q 指针一开始都指向这棵树的根,随后 p 右移时,q 左移,p 左移时,q 右移。每次检查当前 p 和 q 节点的值是否相等,如果相等再判断左右子树是否对称。
代码实现:
1 | |
复杂度分析:
假设树上一共 n 个节点。
1、时间复杂度:这里遍历了这棵树,渐进时间复杂度为 O(n)。
2、空间复杂度:这里的空间复杂度和递归使用的栈空间有关,这里递归层数不超过 n,故渐进空间复杂度为 O(n)。
法二:迭代
「法一」中我们用递归的方法实现了对称性的判断,那么如何用迭代的方法实现呢?首先我们引入一个队列,这是把递归程序改写成迭代程序的常用方法。初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值(队列中每两个连续的结点应该是相等的,而且它们的子树互为镜像),然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时,或者我们检测到树不对称(即从队列中取出两个不相等的连续结点)时,该算法结束。
代码实现:
1 | |
复杂度分析
1、时间复杂度:O(n),同「法一」。
2、空间复杂度:这里需要用一个队列来维护节点,每个节点最多进队一次,出队一次,队列中最多不会超过 n 个点,故渐进空间复杂度为 O(n)。
三、总结
本道算法题难度为简单,我们使用递归和迭代两种方式进行了实现
好了,本篇文章到这里就结束了,感谢你的阅读🤝