多数元素（二十）

一、题目描述

这是 LeetCode 上的第一百六十九题：多数元素，难度为 简单。

Tag：「哈希表」、「数组」、「排序」

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入：nums = [3,2,3]
输出：3

示例 2：

输入：nums = [2,2,1,1,1,2,2]
输出：2

提示：

1、n == nums.length

2、1 <= n <= 5 * 10^4

3、-10^9 <= nums[i] <= 10^9

二、解题思路

法一：哈希表

思路：

我们知道出现次数最多的元素大于 [n/2] 次，所以可以用哈希表来快速统计每个元素出现的次数。

算法：

我们使用哈希映射（HashMap）来存储每个元素以及出现的次数。对于哈希映射中的每个键值对，键表示一个元素，值表示该元素出现的次数。

我们用一个循环遍历数组 nums 并将数组中的每个元素加入哈希映射中。在这之后，我们遍历哈希映射中的所有键值对，返回值最大的键。我们同样也可以在遍历数组 nums 时候使用打擂台的方法，维护最大的值，这样省去了最后对哈希映射的遍历。

代码实现：

class Solution {
    private Map<Integer, Integer> countNums(int[] nums) {
        Map<Integer, Integer> counts = new HashMap<Integer, Integer>();
        for (int num : nums) {
            if (!counts.containsKey(num)) {
                counts.put(num, 1);
            } else {
                counts.put(num, counts.get(num) + 1);
            }
        }
        return counts;
    }

    public int majorityElement(int[] nums) {
        Map<Integer, Integer> counts = countNums(nums);

        Map.Entry<Integer, Integer> majorityEntry = null;
        for (Map.Entry<Integer, Integer> entry : counts.entrySet()) {
            if (majorityEntry == null || entry.getValue() > majorityEntry.getValue()) {
                majorityEntry = entry;
            }
        }

        return majorityEntry.getKey();
    }
}

复杂度分析：

1、时间复杂度：O(n)

2、空间复杂度：O(n)。

法二：排序

思路：

如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序，那么下标为 [n/2] 的元素（下标从 0 开始）一定是众数。

算法：

对于这种算法，我们先将 nums 数组排序，然后返回上文所说的下标对应的元素。下面的图中解释了为什么这种策略是有效的。在下图中，第一个例子是 n 为奇数的情况，第二个例子是 n 为偶数的情况。

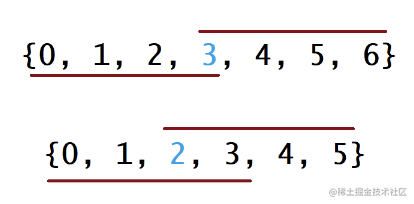
对于每种情况，数组下面的线表示如果众数是数组中的最小值时覆盖的下标，数组下面的线表示如果众数是数组中的最大值时覆盖的下标。对于其他的情况，这条线会在这两种极端情况的中间。对于这两种极端情况，它们会在下标为 [n/2] 的地方有重叠。因此，无论众数是多少，返回 [n/2] 下标对应的值都是正确的。

代码实现：

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length / 2];
    }
}

复杂度分析：

1、时间复杂度：O(nlogn)。将数组排序的时间复杂度为 O(nlogn)。

2、空间复杂度：O(logn)。如果使用语言自带的排序算法，需要使用 O(logn) 的栈空间。如果自己编写堆排序，则只需要使用 O(1) 的额外空间。

三、总结

本道算法题难度为简单，我们使用哈希表和排序两种方式进行了实现

好了，本篇文章到这里就结束了，感谢你的阅读🤝