二叉树的中序遍历（十三）

一、题目描述

这是 LeetCode 热题 HOT 100 上第九十四题：二叉树的中序遍历，难度为 简单。

Tag：「栈」、「树」、「深度优先搜索」、「二叉树」

给定一个二叉树的根节点 root ，返回它的 中序 遍历 。

示例 1：

输入： root = [1,null,2,3]
输出： [1,3,2]

示例 2：

输入： root = []
输出： []

示例 3：

输入： root = [1]
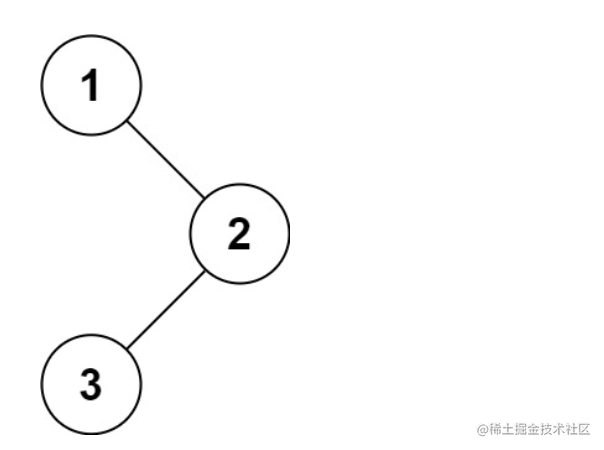
输出： [1]

提示：

1、树中节点数目在范围 [0, 100] 内

2、-100 <= Node.val <= 100

二、解题思路

首先我们应该明白中序遍历的特点：先访问左子树，中间访问根节点，最后访问右子树

接下来我们使用两种方法进行求解：

2.1、法一：递归

1）、按照访问左子树——根节点——右子树的方式遍历这棵树

2）、在访问左子树或右子树的时候，我们按照同样的方式遍历，直到遍历完整棵树

3）、整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程

代码实现：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> keys = new ArrayList<Integer>();
        middleErgodic(root,keys);
        return keys;
    }
    
    private void middleErgodic(TreeNode root,List<Integer> keys){
        if(root == null)return;
        if(root.left != null){
            middleErgodic(root.left,keys);
        }
        
        keys.add(root.val);
        
        if(root.right != null){
            middleErgodic(root.right,keys);
        }
    }
}

时间复杂度和空间复杂度分析：

1、时间复杂度：O(n)，其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。

2、空间复杂度：O(n)。空间复杂度取决于递归的栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。

2.2、法二：迭代

法一的递归我们也可以用迭代的方式实现，两种方式是等价的，区别在于递归隐式地维护了一个栈，而我们在迭代的时候需要显式地将这个栈模拟出来，其他都相同。

代码实现：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> keys = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();
        while(root != null || !stack.isEmpty()){
            while(root != null){
                stack.push(root);
                root = root.left;
            }

            root = stack.pop();
            keys.add(root.val);
            root = root.right;
        }
        return keys;
    }
}

时间复杂度和空间复杂度分析：

1、时间复杂度：O(n)，其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。

2、空间复杂度：O(n)。空间复杂度取决于栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。

依葫芦画瓢：前序遍历，后序遍历，同样可以使用这两种方式进行求解

三、总结

本道算法题难度为简单，我们使用递归，迭代两种方法进行了快速求解，使用这两种方式同样可以解决前序遍历和后序遍历的问题

好了，本篇文章到这里就结束了，感谢你的阅读🤝