线性表之链表上篇

前言

之前我们介绍了使用顺序存储结构实现顺序表，我们发现虽然顺序表的查询很快，时间复杂度为 O(1)，但是增删的效率是比较低的，因为每一次增删操作都伴随着大量的数据元素移动。这个问题有没有解决方案呢？

答：有，我们可以使用另外一种存储结构实现线性表：链式存储结构。

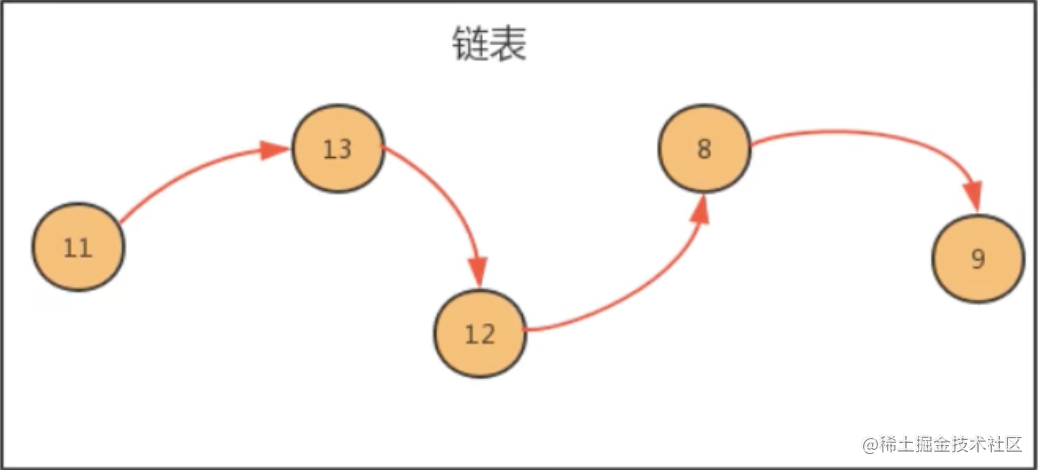
一、链表介绍

链表是一种物理存储单元上非连续，非顺序的存储结构，其物理结构不能直观的表示数据元素的逻辑顺序，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列的节点（链表中的每一个元素称为节点）组成，节点可以运行时动态生成，如下图演示：

image-20221205220501273.png

image-20221205220555432.png

image-20221205220714410.png

那我们如何使用链表呢？按照面向对象的思想，我们可以设计一个类，来描述节点这个事物，用一个属性描述这个节点存储的元素，用另外一个属性描述这个节点的下一个节点。

节点 API 设计：

类名 Node<T>
构造方法 Node(T t,Node next) ：创建 Node 对象
成员变量 T item ：存储数据
Node next ：指向下一个节点

具体实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class Node<T>{
  //存储元素
  public T item;
  //指向下一个节点
  public Node next;
  
  public Node(T item,Node next){
    	this.item = item;
    	this.next = next;
  }
}

//测试：生成链表
public class Test {

    public static void main(String[] args) {
        //构建节点
        Node<Integer> first = new Node<>(11, null);
        Node<Integer> second = new Node<>(13, null);
        Node<Integer> third = new Node<>(12, null);
        Node<Integer> four = new Node<>(8, null);
        Node<Integer> five = new Node<>(9, null);
        
        //生成链表
        first.next = second;
        second.next = third;
        third.next = four;
        four.next = five;
    }
}

链表主要分为两种：

1、单向链表

2、双向链表

二、单向链表

单向链表是链表的一种，它由多个节点组成，每个节点都由一个数据域和一个指针域组成，数据域用来存储数据，指针域用来指向其后继节点。链表的头节点的数据域不存储数据，指针域指向第一个真正存储数据的节点。

image-20221205215218206.png

1.1、单向链表 API 设计

类名 LinkList<T>
构造方法 LinkList() ：创建 LinkList 对象
成员方法 1、public void clean() ：清空线性表
2、public boolean isEmpty() ：线性表是否为空
3、public int length() ：获取线性表元素的个数
4、public T get(int i) ：获取线性表中第 i 个位置元素的值
5、public void insert(int i,T t) ：在第 i 个元素之前插入一个值为 t 的数据元素
6、public void insert(T t) ：向线性表中添加一个元素 t
7、public T remove(int i) ：删除并返回线性表中第 i 个位置的数据元素
8、public int indexOf(T t) ：返回线性表中首次出现的指定的数据元素的位序号，若不存在，则返回 -1
成员内部类 private class Node<T> ：节点类
成员变量 1、private Node head ：记录头节点
2、private int N ：记录链表的长度

具体实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
public class LinkList<T> {

    //记录头节点
    private Node head;
    //记录链表的长度
    private int N;

    private class Node{
        private T item;
        private Node next;

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }

    public LinkList() {
        //初始化头节点
        head = new Node(null, null);
        //初始化元素个数
        this.N = 0;
    }

    public void clear(){
        //将当前头节点的next断掉，那么就找不到这条链表了
        head.next = null;
        //将链表的长度设置为0
        this.N = 0;
    }

    public boolean isEmpty(){
        return this.N == 0;
    }

    public int length(){
        return N;
    }

    public T get(int i){
        //从第 0 个元素开始找，找 i 次，就是第 i 个节点的数据
        Node node = head.next;
        if(node == null) return null;
        for (int i1 = 0; i1 < i; i1++) {
            node = node.next;
        }
        if(node == null) return null;
        return node.item;
    }

    public void insert(T t){
        Node node = head;
        while (node.next != null){
            node = node.next;
        }
        //执行到这里，说明到了尾节点
        //构建一个新的节点
        Node newNode= new Node(t,null);
        //将尾巴节点的 next 指向它
        node.next = newNode;
        //链表长度 +1
        N++;
    }

    public void insert(int index,T t){
        //找到 i 的前一个节点和当前 i 节点
        Node pre = head;
        for (int i = 0; i <= index - 1; i++) {
            pre = pre.next;
        }
        Node current = pre.next;
        //创建新的节点，将前一个节点指向插入的节点，当前插入节点指向下一个节点
        Node newNode = new Node(t, current);
        pre.next = newNode;
        //元素加一
        N++;
    }

    public T remove(int index){
        //找到当前 i 的前一个节点
        Node pre = head;
        for (int i = 0; i <= index - 1; i++) {
            pre = pre.next;
        }
        //找到当前节点
        Node current = pre.next;
        //将前一个节点的 next 指向当前节点的 next
        pre.next = current.next;
        //元素个数减一
        N--;
        return current.item;
    }


    public int indexOf(T t){
        int index = 0;
        Node node = head.next;
        while (node != null){
            if(node.item.equals(t)){
                return index;
            }
            node = node.next;
            index++;
        }
        return -1;
    }
}

1.2、单向链表遍历

在 Java 中，遍历集合的方式一般都是用 foreach 循环，如果想让我们的 SequenceList 也能支持 foreach ，则需要做如下操作：

1、让 LinkList 实现 Iterable 接口，重写 iterator 接口

2、在 LinkList 内部提供一个内部类 LIterator，实现 Iterator 接口，重写 hasNext() 方法和 next() 方法

具体实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
class LinkList<T> implements Iterable<T>{

    //记录头节点
    private Node head;
    //记录链表的长度
    private int N;

    private class Node{
        private T item;
        private Node next;

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }

    public LinkList() {
        //初始化头节点
        head = new Node(null, null);
        //初始化元素个数
        this.N = 0;
    }

    public void clear(){
        //将当前头节点的next断掉，那么就找不到这条链表了
        head.next = null;
        //将链表的长度设置为0
        this.N = 0;
    }

    public boolean isEmpty(){
        return this.N == 0;
    }

    public int length(){
        return N;
    }

    public T get(int i){
        //从第 0 个元素开始找，找 i 次，就是第 i 个节点的数据
        Node node = head.next;
        if(node == null) return null;
        for (int i1 = 0; i1 < i; i1++) {
            node = node.next;
        }
        if(node == null) return null;
        return node.item;
    }

    public void insert(T t){
        Node node = head;
        while (node.next != null){
            node = node.next;
        }
        //执行到这里，说明到了尾节点
        //构建一个新的节点
        Node newNode= new Node(t,null);
        //将尾巴节点的 next 指向它
        node.next = newNode;
        //链表长度 +1
        N++;
    }

    public void insert(int index,T t){
        //找到 i 的前一个节点和当前 i 节点
        Node pre = head;
        for (int i = 0; i <= index - 1; i++) {
            pre = pre.next;
        }
        Node current = pre.next;
        //创建新的节点，将前一个节点指向插入的节点，当前插入节点指向下一个节点
        Node newNode = new Node(t, current);
        pre.next = newNode;
        //元素加一
        N++;
    }

    public T remove(int index){
        //找到当前 i 的前一个节点
        Node pre = head;
        for (int i = 0; i <= index - 1; i++) {
            pre = pre.next;
        }
        //找到当前节点
        Node current = pre.next;
        //将前一个节点的 next 指向当前节点的 next
        pre.next = current.next;
        //元素个数减一
        N--;
        return current.item;
    }


    public int indexOf(T t){
        int index = 0;
        Node node = head.next;
        while (node != null){
            if(node.item.equals(t)){
                return index;
            }
            node = node.next;
            index++;
        }
        return -1;
    }

    //================================== 新增部分代码 start =================================
    @NonNull
    @Override
    public Iterator<T> iterator() {
        return new LIterator();
    }

    private class LIterator implements Iterator<T>{

        private Node curr;

        public LIterator() {
            curr = head;
        }

        @Override
        public boolean hasNext() {
            return curr.next != null;
        }

        @Override
        public T next() {
            curr = curr.next;
            return curr.item;
        }
    }
    //================================== 新增部分代码 end =================================
}

1.3、单向链表测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class Test {

    public static void main(String[] args) {
        LinkList<String> strList = new LinkList<>();
        //1、插入元素
        strList.insert("姚明");
        strList.insert("科比");
        strList.insert("麦迪");
        strList.insert(1,"詹姆斯");
      	//2、遍历
        for (String s : strList) {
            System.out.println(s);
            //姚明
            //詹姆斯
            //科比
            //麦迪
        }
        //3、获取元素
        String result = strList.get(1);
        System.out.println(result);//詹姆斯
        //4、删除元素
        String removeElement = strList.remove(0);
        System.out.println(removeElement);//姚明
        //5、测试清空
        strList.clear();
        System.out.println(strList.length());//0
    }
}

三、单向链表时间复杂度分析

3.1、get(i) 方法时间复杂度

get(i) 每一次查询，都要从链表的头开始，依次向后查询，随着数据元素 N 的增加，比较的元素也越多，时间复杂度为 O(n)

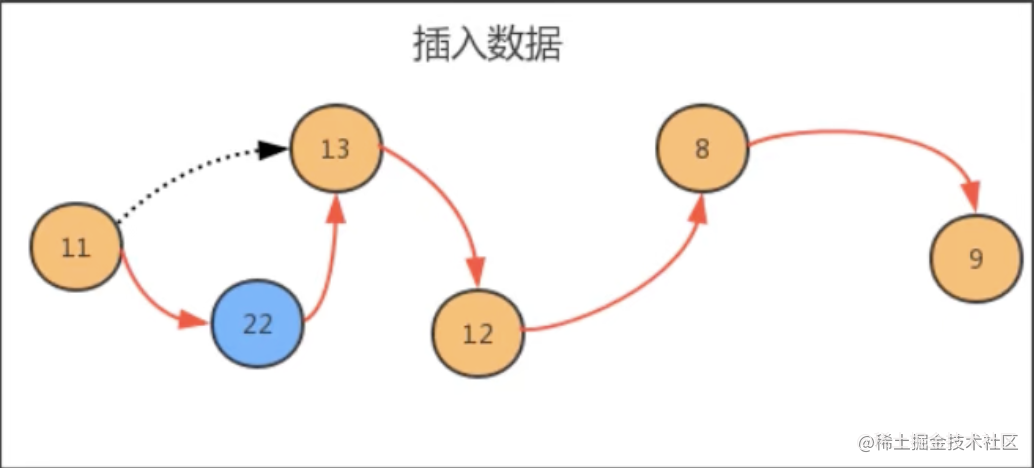
3.2、insert(int i,T t) 方法时间复杂度

insert(int i,T t) 每一次插入，需要先找到 i 位置的前一个元素，然后完成插入操作，随着数据元素 N 的增多，查找的元素越多，时间复杂度为 O(n)

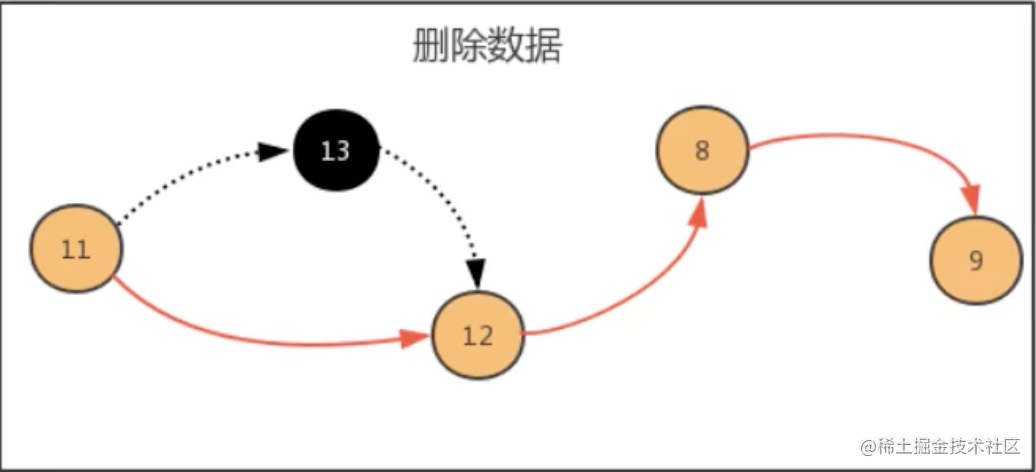
3.3、remove(int i) 方法时间复杂度

remove(int i) 每一次删除，需要先找到 i 位置的前一个元素，然后完成移除操作，随着数据元素 N 的增多，查找的元素越多，时间复杂度为 O(n)

相比较顺序表：

1、链表插入和删除时间复杂度虽然一样，但仍然有很大的优势，因为链表的物理地址是不连续的，它不需要预先指定存储空间大小，或者存储过程中涉及扩容等操作，同时它并没有涉及元素的交换。

2、链表的查询操作性能会比较低，因此如果我们的程序中查询操作比较多，建议使用顺序表，增删操作比较多，建议使用链表。

四、总结

本篇文章我们介绍了：

1、链表的节点及具体实现

2、单向链表的 API 设计，到具体实现，到添加增强 for 循环遍历，到用例测试

3、单向链表的时间复杂度分析：

1、get(i) ：O(n)

2、insert(int i,T t) ：O(n)

3、remove(int i) ：O(n)

虽然链表的插入和删除的时间复杂度和顺序表一样，但是它不需要预先指定存储空间以及扩容等操作，效率还是很高的，因此涉及到增删比较多的情况使用链表，查询比较多的则使用顺序表

好了，本篇文章到这里就结束了，感谢你的阅读🤝

数据结构和算法 > 数据结构
#原创 #数据结构和算法
线性表之链表上篇
https://sweetying520.github.io/2022/08/04/D2.1-线性表之链表上篇/
作者
sweetying
发布于
2022年8月4日
许可协议