选择排序和插入排序（三）

一、选择排序

选择排序是一种更加简单直观的排序方法

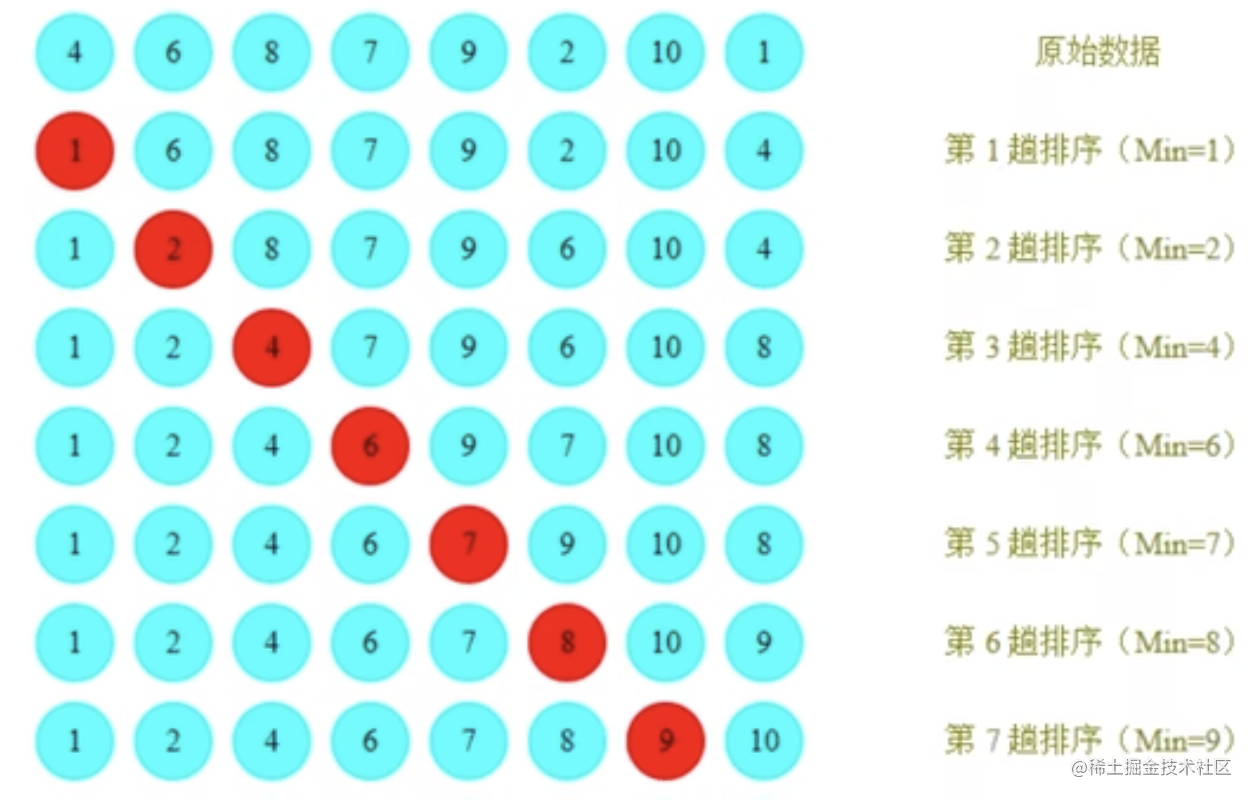
需求：

排序前：{4,6,8,7,9,2,10,1}

排序后：{1,2,4,5,7,8,9,10}

排序原理：

1、每一次在遍历过程中，都假定第一个索引处的元素是最小值，和其他索引处的值依次进行比较，如果当前索引处的值大于其他某个索引处的值，则假定其他某个索引处的值为最小值，最后可以找到最小值所在的索引。

2、交换第一个索引处和最小值所在的索引处的值

了解了原理，接下来我们通过代码实现一下它：

//1、编写一个选择排序的类
class Selection{

    public static void sort(Comparable[] a){
        final int length = a.length;
        //外层循环需要执行 length - 1 次
        for (int i = 0; i < length - 1; i++) {
            //声明一个最小索引，用于和 i 位置处的元素进行交换
            int minIndex = i;
            //外层循环每执行一次，内层循环需执行 length - i 次来确定最小索引
            for(int j = i + 1; j < length; j++){
                //如果前一个数大于后一个数，则使用 minIndex 记录较小值的索引
                if(greater(a[minIndex],a[j])){
                    minIndex = j;
                }
            }
            //交换 minIndex 和 i 位置元素的值
            exchange(a,i,minIndex);
        }
    }

    /**
     * 比较两个数的大小
     */
    public static boolean greater(Comparable c1,Comparable c2){
        return c1.compareTo(c2) > 0;
    }

    /**
     * 交换 i，j 位置的值
     */
    public static void exchange(Comparable[] a,int i,int j){
        Comparable temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

//2、测试
public class Test {

    public static void main(String[] args) {
       Integer[] intArray = {4,6,8,7,9,2,10,1};
       Selection.sort(intArray);
       System.out.println(Arrays.toString(intArray));
    }
}

//打印结果
[1, 2, 4, 6, 7, 8, 9, 10]

选择排序的时间复杂度分析：

选择排序使用了双层 for 循环，其中外层循环完成了数据交换，内层循环完成了数据比较，所以我们分别统计数据交换次数和数据比较次数：

数据比较次数：

1 + 2 + 3 + 4… + (N - 2) + (N - 1) = N^2/2 - N/2

数据交换次数：

N - 1

时间复杂度：N^2/2 - N/2 + (N - 1) = N^2/2 + N/2 - 1

根据大 O 表示法推导，保留最高阶项，去除常数因子，时间复杂度为：O(N^2)

二、插入排序

插入排序（Insertion sort）是一种简单直观且稳定的排序算法

插入排序的工作方式非常像人们排序一手扑克牌一样，开始时，我们左手为空并且桌子上的牌面朝下。然后，我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置，我们从右到左将它与已在手中的每张牌进行比较。

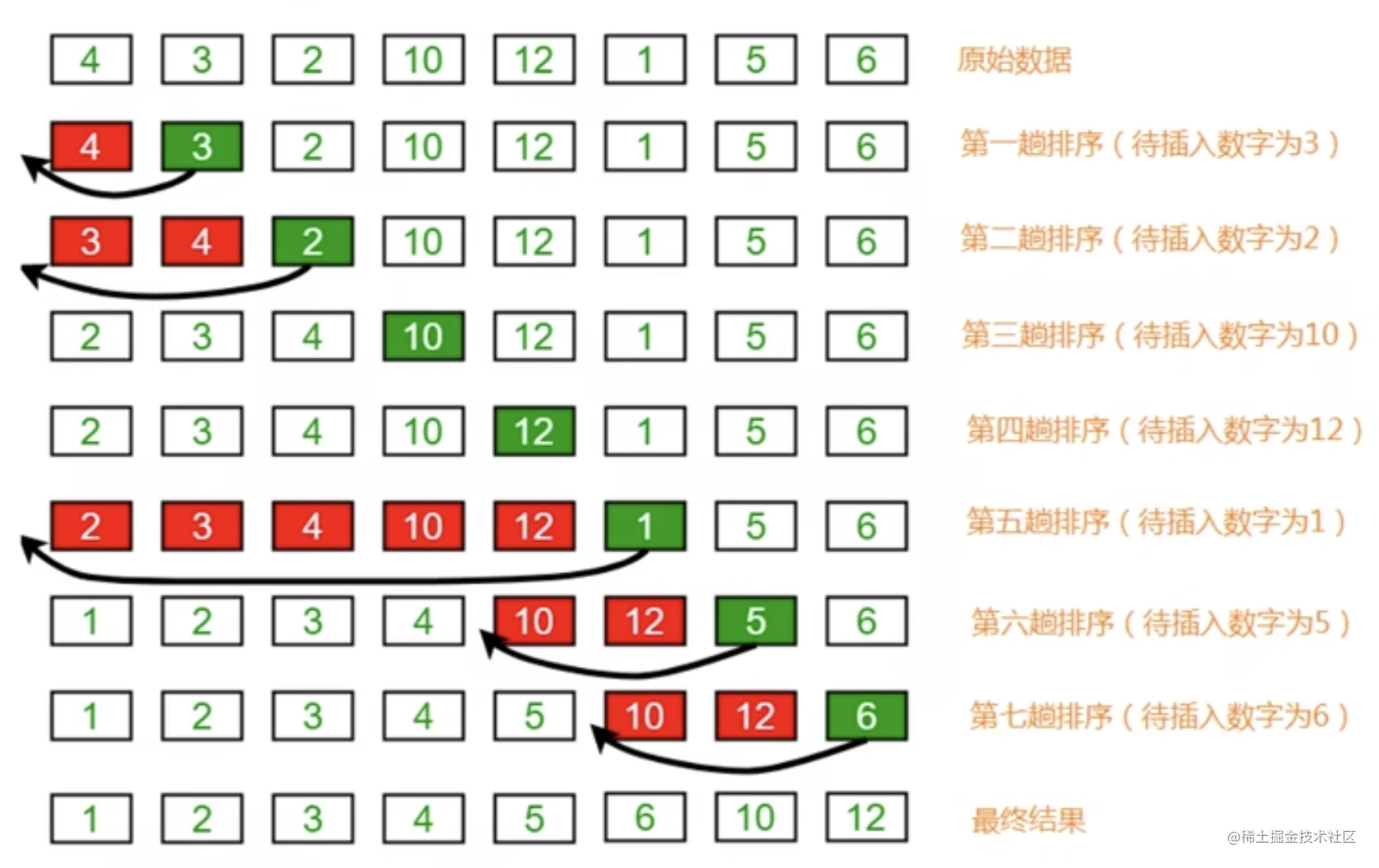
需求：

排序前：{4,3,2,10,12,1,5,6}

排序后：{1,2,3,4,5,6,10,12}

排序原理：

1、把所有的元素分为两组，已经排序的和未排序的。

2、找到未排序组中的第一个元素，向已经排序的组中进行插入。

3、倒序遍历已经排序的元素，依次和待插入的元素进行比较，直到找到一个元素小于等于待插入元素，那么就把待插入元素放到这个位置，其他的元素向后移动一位。

了解了原理，接下来我们通过代码实现一下它：

//1、编写一个插入排序的类
class Insertion{

    public static void sort(Comparable[] a){
        final int length = a.length;
        for (int i = 1; i < length; i++) {
            //当前元素 a[i] ，依次和 i 前面的元素比较，找到一个小于等于 a[i] 的元素时，进行交换
            for(int j = i; j > 0; j--){
                if(greater(a[j-1],a[j])){
                    //交换元素
                    exchange(a,j-1,j);
                }else{
                    //找到了该元素，结束内层 for 循环
                    break;
                }
            }
        }
    }

    /**
     * 比较两个数的大小
     */
    public static boolean greater(Comparable c1,Comparable c2){
        return c1.compareTo(c2) > 0;
    }

    /**
     * 交换 i，j 位置的值
     */
    public static void exchange(Comparable[] a,int i,int j){
        Comparable temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

//2、测试
public class Test {

    public static void main(String[] args) {
       Integer[] intArray = {4,3,2,10,12,1,5,6};
       Insertion.sort(intArray);
       System.out.println(Arrays.toString(intArray));
    }
}

//打印结果
[1, 2, 3, 4, 5, 6, 10, 12]

插入排序时间复杂度分析：

插入排序使用了双层 for 循环，其中内层循环的循环体是真正完成排序的代码，所以，我们分析插入排序的时间复杂度，主要分析一下内层循环体的执行次数即可。

最坏情况，也就是待排序的数组元素为 {12,10,6,5,4,3,2,1}，那么：

比较的次数为：

1 + 2 + 3 + …(N - 2) + (N - 1) = N^2 / 2 - N / 2

交换的次数：

1 + 2 + 3 + …(N - 2) + (N - 1) = N^2 / 2 - N / 2

总执行次数：

N^2 / 2 - N / 2 + N^2 / 2 - N / 2 = N^2 - N

根据大 O 表示法推导，保留最高阶项，时间复杂度为：O(N^2)

三、总结

本篇文章我们介绍了：

1、选择排序原理，实际案例编写，以及时间复杂度分析

2、插入排序原理，实际案例编写，以及时间复杂度分析

好了，本篇文章到这里就结束了，感谢你的阅读🤝